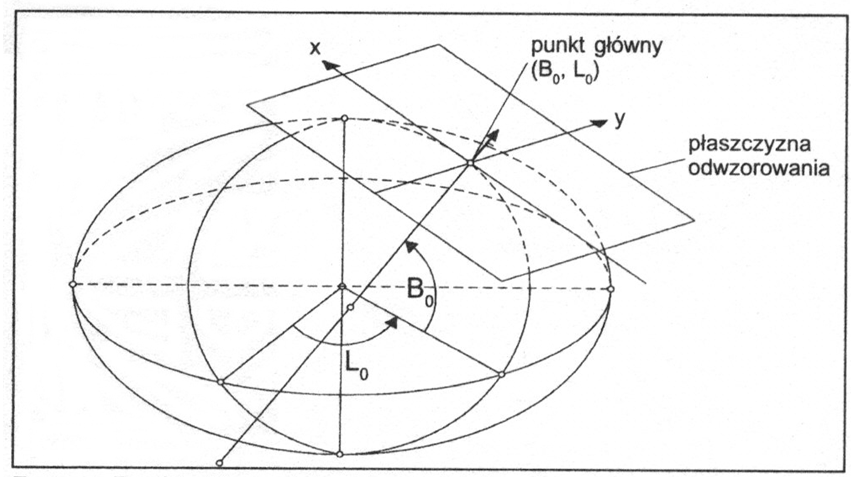
Odwzorowanie quasi-stereograficzne WIG (Wojskowego Instytutu Geograficznego) jest równokątnym, azymutalnym odwzorowaniem powierzchni elipsoidy obrotowej na płaszczyznę. Odpowiada ono stereograficznemu odwzorowaniu kuli o promieniu
Ro = √Mo No
gdzie:
Mo – promień krzywizny południka
No – promień krzywizny przekroju poprzecznego I wertykału dla centralnej szerokości.
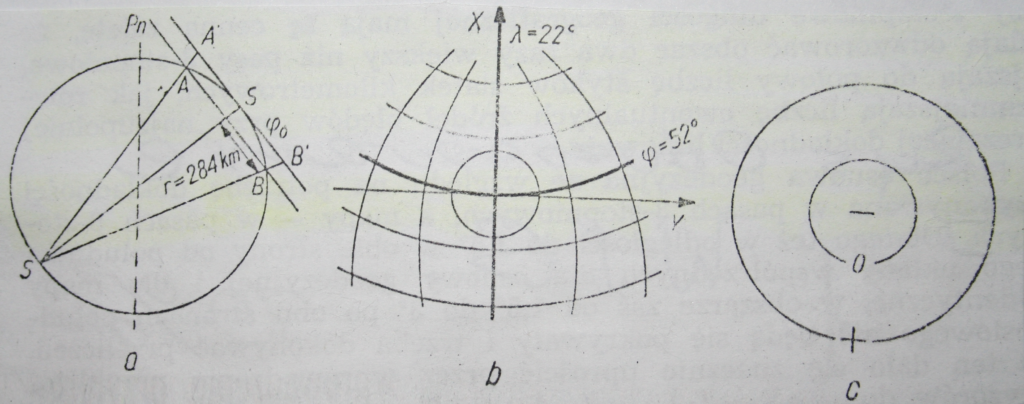
Siatka geograficzna odwzorowuje się na płaszczyźnie jako zespół krzywych, bardzo mało różniących się od łuków kół. W celu zmniejszenia bezwzględnej wartości zniekształceń liniowych w odwzorowaniu płaskim zmniejsza się promień Ro kuli w pewnym niewielkim stosunku, zwanym stałą skali. Przy zastosowaniu tej stałej płaszczyzna odwzorowania staje się płaszczyzną sieczną (rys.4 a). W ten sposób można zmniejszyć do połowy bezwzględną wartość zniekształceń długości.
Metodę tego typu odwzorowania stereograficznego dla elipsoidy podał w 1924 roku astronom francuski Roussilhe, tworząc odwzorowanie równokątne i azymutalne. Oparł się on na założeniu, że zniekształcenia długości powinny wynosić maksimum 1:1000 w obszarze o promieniu 500 km od punktu głównego oraz że obliczenia tych zniekształceń powinny być proste.
Profesor dr Lucjan Grabowski z Politechniki Lwowskiej uprościł wyprowadzenie wzorów matematycznych dla odwzorowania Roussilhe’a, a oficerowie WIG F. Biernacki i J. Słomczyński w 1930 roku zastosowali to odwzorowanie do obszaru Polski.
Odwzorowanie Roussilhe’a zmodyfikowane dla terenu Polski nazwano odwzorowaniem quasi-stereograficznym Wojskowego Instytutu Geograficznego (rys. 4 b).
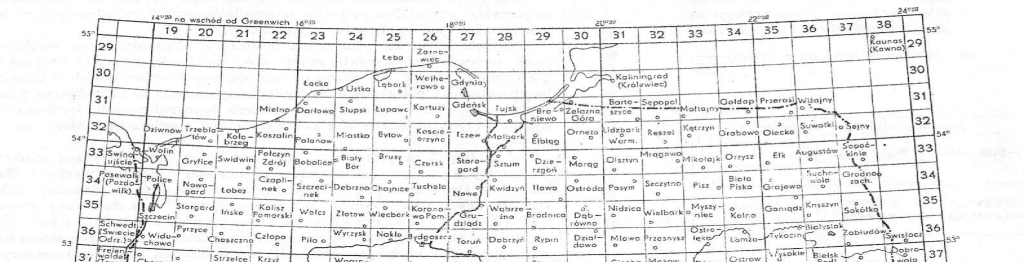
Odwzorowanie to było podstawą do konstrukcji polskich map topograficznych w okresie międzywojennym. Punkt główny odwzorowania quasi-stereograficznego WIG obrano
w punkcie o współrzędnych: φ = 52° , λ = 22° E.Gr.
Płaszczyzna odwzorowania wskutek zastosowania stałej skali równej 1:2000 (skurczenie lub zmniejszenie w stosunku 0,9995) stała się płaszczyzną sieczną przecinającą elipsoidę wzdłuż elipsy zbliżonej do okręgu koła o promieniu około 284 km od punktu głównego (rys.4 b). Na obwodzie koła nie ma zniekształceń długości, wewnątrz koła występuje skurczenie, a na zewnątrz koła rozciągnięcie obszaru podlegającego odwzorowaniu (rys.4 c).
Odwzorowanie to jest szczególnie przydatne do przedstawiania obszarów, których granice mają kształt regularny, zbliżony do okręgu leżących w szerokościach umiarkowanych. Punkt główny odwzorowania powinien znajdować się w pobliżu punktu środkowego odwzorowywanego obszaru (rys.5). Południk przechodzący przez punkt główny nazywany jest południkiem środkowym. Południk środkowy odwzorowuje się jako odcinek linii prostej.